Skip to main content

Path difference and Phase difference



Path difference is the difference in path traversed by the two waves , measured in terms of wavelength of the associated wave. It has a direct relation with phase difference. Phase difference decides the nature of interference pattern but phase difference is found out by path difference.

Let's assume that, two stones are thrown at two points which are very near, then you will see the following pattern as shown in the figure below:


Eg:





let's mark the first point of disturbance as S1S1 and the other as S2S2, then waves will be emanated as shown above. By having a cross-sectional view, you will see the same waves as shown in the figure below (in the below explanation wavelengths of waves emanated from two different disturbances is assumed to be the same).
The waves emanating from S1S1 has arrived exactly one cycle earlier than the waves from S2S2. Thus, we say that, there is a path difference between the two waves of about λλ (wavelength). If the distance traveled by the waves from two disturbance is same, then path difference will be zero. Once you know the path difference, you can find the phase difference using the formula given below:

 ΔX=λ⋅Δϕ2π

 Here, ΔX is path difference, Δϕ is phase difference.
path difference is the difference in path traversed by the two waves , measured in terms of wavelength of the associated wave. It has a direct relation with phase difference. Phase difference decides the nature of interference pattern but phase difference is found out by path difference. Phase difference is related to quantum mechanics. If path difference b/w 2 waves is integral multiple of wavelength, which satisfies condition for constructive interference. Whereas, if path difference b/w 2 waves is odd multiple of half wavelength, it satisfies condition for destructive interference.

 whereas phase difference is the difference between some reference point in 2 waves. Its how much one wave is shifted from the other. For eg. at the origin, if one wave's displacement is zero and the other one has some displacement, then there is a shift, which is their phase difference. For eg. sine wave is zero at the origin, but cos wave is not zero at the origin, its zero at pi/2. So the phase difference is pi/2. Infact, cos wave is just the sine wave phase-shifted.

 If two waves have zero phase difference, then their crests occur at the same time and so do their troughs. Its like moving together. They will add up (constructive interference).

 For only one wave, phase difference means how much the wave is shifted from the origin. Like in your example, Acos(wt + Φ), at time t=0, cos has some value other than 1. So, the cos wave is slightly shifted by Φ. Physically, what this means is when u started measuring the time, the system oscillates, not from either origin or amplitude, but somewhere in between.
Ofcourse, the concept of phase difference is not useful if there is only one wave. You could always choose time to start from when the system is at an extreme position. Phase difference concept is useful when there are atleast 2 waves, then when u start the time when one wave starts from zero, the other wave could already be in some other position.

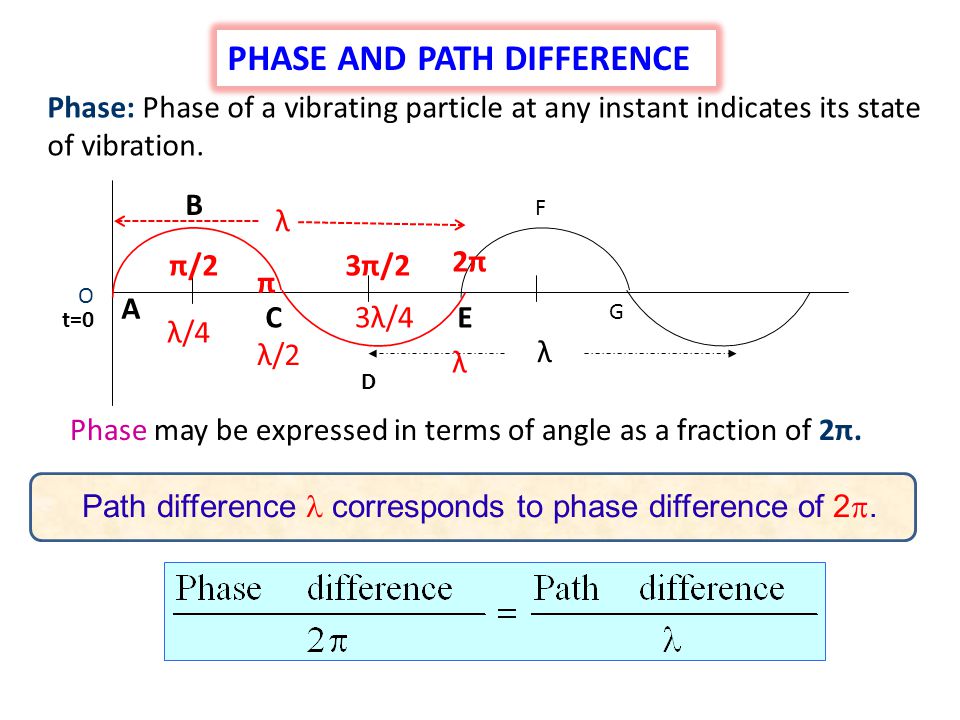
Phase Difference

Look at the diagram below of a progressive wave moving left to right.


Imagine you are particle B – in what vertical direction are you moving?

 UP!

 Now look at a particle a whole wavelength further along the wave (particle F).  What direction is it moving?

 UP!
Not only are they oscillating in the same direction, but they oscillate in time with each other.




Path Difference


The path difference of two waves is the difference in distance that the waves have traveled.




So how does the path difference of two waves link to phase difference?

Remember above we said that you could work out the phase difference of two waves of identical wavelength by working out the separation in terms of fraction of a wavelength?



Well we can use the same principal for any two waves of identical wavelength arriving at a point:

Path difference = integer number of wavelengths = IN PHASE



Path difference = 1/2 number of wavelengths = ANTIPHASE





Linking Path Difference and Phase Difference: Equation

pdpd1NOTE: Convert both the path difference AND the wavelength into metres first! And leave radians in terms of pi!



Popular posts from this blog

Interference in Wedge Shaped Film (Reflected Rays)

Thin Film Interference A film of thickness from 0.5 to 10  m is a transparent medium of glass, mica, air enclosed between glass, soap film, etc. When the light is made incident on this thin film partial reflection and partial refraction occur from the top surface of the film. The refracted beam travels in the medium and again suffers partial reflection and partial refraction at the bottom surface of the film. In this way several reflected and refracted rays are produces by a single incident ray. As they moves are superimposed on each other and produces interference pattern. Interference in Parallel Film ( Reflected Rays) Consider a thin film of uniform thickness ‘t’ and refractive index   bounded between air. Let us consider monochromatic ray AB is made incident on the film, at B part of ray is reflected (R 1 ) and a part is refracted along BC.At C The beam BC again suffer partial reflection and partial refraction,  the reflected beam CD mov...
Read more

Lloyd's’ mirror experiment

Lloyd's mirror This is another method for finding the wavelength of light by the division of wavefront. Light from a slit So falls on a silvered surface at a very small grazing angle of incidence as shown in the diagram (Figure 1). A virtual image of So is formed at S1. Interference occurs between the direct beam from So to the observer (0) and the reflected beam The zeroth fringe will be black because of the phase change due to reflection at the surface.  Application An interesting application of this effect may be observed when a helicopter flies above the sea near a radio transmitter. The helicopter will receive two signals: (a) one signal directly from the transmitter and (b) a second signal after reflection from the sea As the helicopter rises the phase difference between the two signals will alter and the helicopter will pass through regions of maxima and minima. Lloyd's mirror Experiment Lloyd’s Mirror is used to produce two-source interference...
Read more

Thin-Lens Equation:Newtonian Form

In the Newtonian form of the lens equation, the distances from the focal length points to the object and image are used rather than the distances from the lens. Newton used the "extrafocal distances" xo and xi in his formulation of the thin lens equation. It is an equivalent treatment, but the Gaussian form will be used in this resource.
Read more